... Allah hat allem sein Maß bestimmt. (Surat 65:3 - at-Talaq)

...Du erblickst in der Schöpfung des Erbarmers kein Missverhältnis. So schau dich von neuem um, ob du Mängel siehst! Dann lass den Blick ein weiteres Mal schweifen - jedes Mal wird dein Blick stumpf und matt zu dir zurückkehren. (Sure 67:3, 4 –al-Mulk)

Wenn eine ästhetische, äusserst ausgewogene Form der Elemente eines Objekts oder einer Funktion erreicht wird, dann sehen wir höchstwahrscheinlich etwas, das auf der Goldenen Zahl basiert. Die Goldene Zahl ist kein Phantasieprodukt falsch angewandter Mathematik, sondern sie entspringt einem natürlichen Prinzip, das mit den Gesetzen des Gleichgewichts in Verbindung steht. (1)
Was haben die ägyptischen Pyramiden, Leonardo Da Vinci’s Porträit der Mona Lisa, Sonnenblumen, die Schnecke, der Kiefernzapfen und Ihre Finger gemeinsam?
Die Antwort auf diese Frage liegt in einer Zahlenreihe verborgen, die von dem italienischen Mathematiker Fibonacci entdeckt worden ist. Die Eigenschaft der Fibonacci-Zahlen ist, das jede aus der Summe ihrer zwei vorhergehenden Zahlen besteht. (2)

Fibonacci Zahlen

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, …

Fibonacci Zahlen haben jedoch noch eine weitere, ganz besondere Eigenschaft: Wenn man die Zahlen der Reihe jeweils durch die ihr vorhergehende Zahl dividiert, erhält man Ergebnisse, die bis in die dritte Stelle hinter dem Komma identisch sind. Das Ergebnis ab der dreizehnten Zahl in der Reihe bleibt sogar konstant. Diese Zahl ist die “Goldene Proportion”.

GOLDENE PROPORTION = 1.618

233 / 144 = 1.618

377 / 233 = 1.618

610 / 377 = 1.618

987 / 610 = 1.618

1597 / 987 = 1.618

2584 / 1597 = 1.618

DER MENSCHLICHE KÖRPER UND DIE GOLDENE PROPORTION

Bei der Durchführung ihrer Forschungen und der Auslegung ihrer Produkte beziehen sich Künstler, Wissenschaftler und Designer auf den menschlichen Körper, dessen Proportionen der Goldenen Proportion entsprechen, als Maßstab. Leonardo da Vinci und Le Corbusier legten ihren Designs den menschlichen Körper zugrunde. Auch der „Neufert“, eines der wichtigsten Referenzwerke über moderne Architektur, nimmt den menschlichen Körper als Basis.

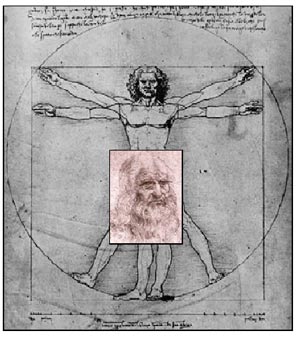
Leonardo da Vinci hat die Goldene Proportion für den menschlichen Körper benutzt.

 

DIE GOLDENE PROPORTION IM MENSCHLICHEN KÖRPER

Die “idealen” proportionalen Beziehungen, die zwischen den unterschiedlichen Teilen des durchschnittlichen menschlichen Körpers bestehen, können allgemein wie folgt beschrieben werden: (3)

Das M/m Niveau in der untenstehenden Tabelle entspricht immer der Goldenen Proportion. M/m = 1,618

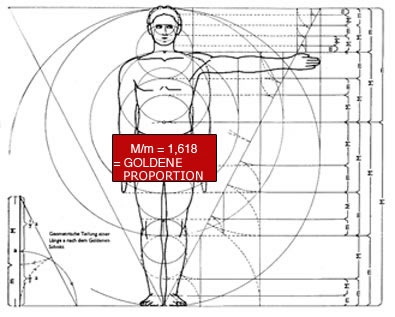
Das erste Beispiel für die Goldene Proportion im durchschnittlichen menschlichen Körper ist der Abstand zwischen Nabel und Fuß. Setzt man diesen mit 1 gleich, so entspricht die Größe eines Menschen 1,618. Weitere Goldene Proportionen des durchschnittlichen menschlichen Körpers sind:

der Abstand zwischen Fingerspitze und Ellbogen und der Abstand zwischen Handgelenk und Ellbogen,
der Abstand zwischen der Schulterlinie und der Schädeldecke und das Schädel-Längsmaß,
Der Abstand zwischen Nabel und Schädeldecke und der Abstand zwischen Schulterlinie und Schädeldecke,
Der Abstand zwischen Nabel und Knie und der Abstand zwischen Knie und Fußsohle

Die menschliche Hand

Nehmen Sie die Hand von der Computermaus und betrachten Sie die Form Ihres Zeigefingers. Aller Wahrscheinlichkeit nach sehen Sie eine Goldene Proportion.

Unsere Finger bestehen aus drei Abschnitten. Die Proportion der ersten beiden zur vollen Länge des Fingers ist eine Goldene Proportion, mit Ausnahme der Daumen. Sie können auch sehen, dass das Größenverhältnis des Mittelfingers zum kleinen Finger eine Goldene Proportion ist.(4)

Sie haben zwei Hände, und deren Finger bestehen aus drei Abschnitten. Es gibt fünf Finger an jeder Hand und nur acht von ihnen gliedern sich entsprechend der Goldenen Proportion: 2, 3, 5 und 8 gehören zu den Fibonacci Zahlen.

Die Goldene Proportion im Gesicht des Menschen

Es gibt verschiedene Goldene Proportionen im menschlichen Gesicht. Sie sind jedoch nicht mit dem Lineal messbar, denn sie beziehen sich auf das „ideale menschliche Gesicht“ nach den Vorstellungen von Wissenschaftlern und Künstlern.

Zum Beispiel ergibt das Verhältnis der Breite der beiden Frontzähne des Oberkiefers zu ihrer Länge eine Goldene Proportion. Der Breite des ersten Zahns von der Mitte zum zweiten Zahn ergibt ebenfalls eine Goldene Proportion. Dies könnten in den Augen eines Zahnarztes die idealen Proportionen sein. Andere Goldene Proportionen des menschlichen Gesichts sind:

Länge des Gesichts / Breite des Gesichts,
Abstand zwischen den Lippen und dem imaginären Punkt, an dem sich die Augenbrauen treffen würden / Nasenlänge
Länge des Gesichts / Abstand zwischen Kinnspitze und dem imaginären Punkt, an dem sich die Augenbrauen treffen würden
Breite des Mundes / Breite der Nase
Breite der Nase / Abstand zwischen den Nasenlöchern
Abstand zwischen den Pupillen / Abstand zwischen den Augenbrauen

Goldene Proportion in den Lungen

In einer zwischen 1985 und 1987 durchgeführten Studie (5),fanden die amerikanischen Physiker B. J. West und Dr. A. L. Goldberger die Existenz der Goldenen Proportion in der Lungenanatomie. Ein Merkmal des bronchialen Netzwerks der Lunge ist seine Asymmetrie. Die Luftröhre teilt sich in zwei Hauptbronchien, eine lange auf der linken Seite und eine kurze auf der rechten Seite. Diese asymmetrische Aufteilung setzt sich in der weiteren Verästelung der Bronchien fort. (6)

Man stellte fest, dass das Verhältnis der kurzen zu den langen Bronchien immer 1 zu 1, 618 beträgt.

DAS GOLDENE RECHTECK UND DAS DESIGN DER SPIRALE

Ein Rechteck mit einem Seitenverhältnis, das der Goldenen Proportion entspricht, ist ein “Goldenes Rechteck“. Angenommen, entlang einer der beiden kurzen Seiten eines Rechtecks sei ein Quadrat in das Rechteck eingezeichnet, und in diesem Quadrat befinde sich ein Viertelkreis dergestalt eingezeichnet, dass ein Ende des Viertelkreises in eine der Längsseiten des Rechtecks ausläuft. Nun zeichnen wir ein weiteres Quadrat in den verbleibenden kleineren Teil des ursprünglichen Rechtecks und in dieses neue Rechteck wieder einen Viertelkreis, der an den Viertelkreis des ersten Quadrats anschließt. Wenn wir dies für alle auf diese Weise verbleibenden Rechtecke innerhalb des Ausgangsrechtecks tun würden, so erhielten wir eine Spirale.

Der britische Ästhetiker William Charlton erklärt, dass die Menschen Vergnügen an einer Spirale empfinden, weil man ihr visuell ganz leicht folgen kann. (7)

Die auf der Goldenen Proportion basierenden Spiralen enthalten ein unvergleichliches Design in der Natur. Beispiele hierfür sind die Spiralsequenzen der Sonnenblume und der Kiefernzapfen. Der Wachstumsprozess vieler Lebewesen findet ebenfalls in einer logarithmischen Spiralform statt. Die Form der „Kurven“ der Spirale ist immer gleich, und die Proportionen der Gesamtform ändern sich nicht, unabhängig von ihrer Größe. Keine andere Form in der Mathematik besitzt diese Eigenschaft. All das ist ein Beispiel für die makellose Schöpfung des allmächtigen Gottes und dafür, wie Er alles nach einem bestimmten Maß erschaffen hat. (8)

Das Design der Seemuscheln

Das fehlerlose Design im Nautilus enthält die Goldene Proportion.

Bei der Untersuchung der Schalen von Mollusken, die am Meeresgrund leben, erregten Form und Struktur der inneren und äußeren Oberflächen die Aufmerksamkeit der Wissenschaftler:

Die innere Oberfläche ist glatt, die äußere gerillt. Der Körper der Molluske befindet sich in der Schale, daher sollte deren Innenseite glatt sein. Die äußeren Kanten der Schalen erhöhen deren Festigkeit und verstärken so ihre Stabilität. Die Schalenformen erstaunen durch ihre Perfektion und den sparsamen Materialeinsatz bei ihrer Schöpfung. Die Spiralform der Muschel ist in perfekter geometrischer Form ausgedrückt, in einem überraschend schönen, geschliffenen Design.(9)

Die Schalen der meisten Muscheln wachsen in einer logarithmischen Spirale. Nun kann jedoch kein Zweifel daran bestehen, dass diese Tiere nicht die geringsten Fähigkeiten zu mathematischen Kalkulationen haben, von logarithmischen Funktionen gar nicht zu sprechen. Wie ist es also möglich, dass diese Kreaturen wissen, wie sie am besten wachsen? Wie können diese Tiere, die von manchen Wissenschaftlern als „primitiv“ bezeichnet werden, wissen, dass dies die Idealform für sie ist? Ein solches Wachstum kann unmöglich in Abwesenheit von Bewusstsein und Intellekt stattfinden. Doch dieses Bewusstsein steckt weder in den Mollusken, noch - wie manche Wissenschaftler behaupten - in der Natur selbst. Es ist völlig irrational, in den Kategorien des Zufalls danach zu suchen. Dieses Design kann nur das Produkt eines überlegenen Intellekts mit unendlicher Weisheit sein und es gehört dem allmächtigen Allah, dem Schöpfer aller Dinge.

Mein Herr umfasst alle Dinge mit Seinem Wissen. Wollt ihr euch denn nicht ermahnen lassen?  (Sure 6:80 – al-An‘am)

Wachstum dieser Art wurde von dem Biologen Sir D’Arcy Thompson, einem Experten auf diesem Gebiet, als „gnomisches Wachstum“ bezeichnet. Er führte aus, es sei unmöglich, sich ein einfacheres System vorzustellen während des Wachstums einer Seemuschel, als ein auf Erweiterung und Ausdehnung mit identischen und unveränderlichen Proportionen beruhendes System, wobei die Muschel ständig wächst, aber deren Form konstant bleibt. (10)

Eines der besten Beispiele dafür ist der Nautilus, nur wenige Zentimeter im Durchmesser. C. Morrison beschreibt diesen Wachstumsprozess, der selbst für eine menschliche Intelligenz außergewöhnlich schwer zu planen wäre: In der Nautilusschale befindet sich eine innere Spirale mit aus Perlmutt bestehenden Kammern. Während des Wachstums des Tieres entstehen immer größere Kammern am Ende der Spirale und das Tier „zieht um“ in die jeweils größere Kammer, wobei es die nun verlassene Kammer mit einer Perlmuttschicht verschließt.(11)

Es gibt noch weitere Meeresbewohner mit logarithmisch-spiralförmig aufgebauten Schalen:

Haliotis Parvus, Dolium Perdix, Murex, Fusus Antiquus, Scalari Pretiosa, Solarium Trochleare.

Auch Ammoniten, heute ausgestorbene Seetiere, von denen man nur noch Fossilien findet, hatten in logarithmischen Spiralen wachsende Schalen.

Doch spiralförmiges Wachstum in der Tierwelt beschränkt sich nicht auf die Schalen von Mollusken. Auch Antilopen, Ziegen und Widder entwickeln ihre Hörner in einer Spiralform, die auf der Goldenen Proportion basiert. (12)

Die Goldene Proportion im Gehör- und Gleichgewichtsorgan. Die Cochlea im Innenohr des Menschen dient der Übertragung von Schallwellen. Diese flüssigkeitgefüllte Knochenstruktur hat eine logarithmisch spiralförmige Form mit einem fixen Winkel von 73°43´, was der Goldenen Proportion entspricht.

Spiralförmig wachsende Hörner und Zähne
Beispiele von auf logarithmischen Spiralen basierenden Krümmungen können an den Stoßzähnen von Elefanten und den heute ausgestorbenen Mammuts beobachtet werden, an Löwenklauen und Papageienschnäbeln. Die Eperia-Spinne webt ihre Netze in einer logarithmischen Spirale. Auch die Körper der im Meer lebenden Mikroorganismen Globigerinae, Planorbis, Vortex, Terebra, Turitellae und Trochida, allesamt Planktonarten, sind spiralförmig aufgebaut.

DIE GOLDENE PROPORTION IN DER MIKROWELT

Geometrische Formen beschränken sich nicht auf Dreiecke, Quadrate, Pentagone oder Hexagone. Diese Formen können sich frei kombinieren und ergeben neu dreidimensionale geometrische Formen. Der Würfel und die Pyramide sind die einfachsten Beipiele dafür. Weiterhin gibt es Formen wie den Tetraeder mit vier Flächen, den achtflächigen Octaeder, den Dodekaeder und den Ikosaeder, die im alltäglichen Leben nicht anzutreffen sind und von denen wir vielleicht noch nie gehört haben. Der Dodekaeder besteht aus 12 achteckigen Flächen und der Ikosaeder aus 20 Dreicken. Wissenschaftler haben entdeckt, dass all diese Formen mathematisch ineinander umgewandelt werden können und das diese Transformationen in Verhältnissen geschehen, die der Goldenen Proportion entsprechen.

Dreidimensionale Formen mit der Goldenen Proportion sind sehr weit verbreitet bei Mikroorganismen. Viele Viren haben haben die Icosaeder-Form. Der bekannteste von ihnen ist der Adeno-Virus. Der Proteinmantel des Adeno-Virus besteht aus 252 regelmäßig angeordneten Protein-Untereinheiten. Die 12 Untereinheiten in den Ecken des Icosaeders haben die Form achteckiger Prismen. Stabähnliche Strukturen ragen aus diesen Ecken.

 

Die ersten, die entdeckten, dass Viren in Formen auftreten, die die Goldene Proportion enthalten, waren Aaron Klug und Donald Caspar vom Birkbeck College in London in the 1950er Jahren. (13) Das erste Virus, bei dem sie dies feststellten, war das Polio-Virus. Das Rhino 14 Virus hat dieselbe Form.

Warum treten Viren in Formen auf, die der Goldenen Proportion entsprechen, Formen, die wir nur schwer geistig visualisieren können? Aaron Klug, der Entdecker dieser Formen, erklärt:Mein Kollege Donald Caspar und ich zeigten, dass man das Design dieser Viren mit einer Generalisierung icosaedraler Symmetrie erklären kann, die es erlaubt, dass identische Einheiten Beziehungen zueinander aufbauen können, unter Wahrung eines geringen Maßes an interner Flexibilität. Wir haben alle möglichen Designformen aufgezählt, die Ähnlichkeiten mit den geodesischen Domen des Architekten R. Buckminster Fuller aufweisen. Doch wo Fuller's Dome unter Befolgung eines sorgfältig ausgearbeiteten Codes zusammengebaut werden, entsteht das Design der Virushülle von selbst.(14)

Klug’s Beschreibung offenbart erneut eine offensichtliche Wahrheit. Es gibt eine genaue Planung und eine intelligente Schöpfung, sogar bei Viren, die von Wissenschaftlern als die „einfachsten und primitivsten“ Lebewesen angesehen werden.(15) Dieses Design ist wesentlich erfolgreicher und höher entwickelt, als das des weltbekannten Stararchitekten Buckminster Fuller.

Der Dodekaeder und der Icosaeder tauchen auch beim Kieselsäure-Skelett der Radiolaren auf, bei einzelligen Meeresorganismen.

Strukturen, die auf diesen beiden geometrischen Formen basieren, wie der Dodekaeder mit fußähnlichen Strukturen, die aus jede Ecke ragen, und die verschiedenen Ausformungen an ihrer Oberfläche sorgen für die unterschiedlichen, schön anzusehenden Körper der Radiolarien.(16)

Als Beispiele dieser weniger als einen Millimeter großen Organismen können wir den auf dem Icosaeder basierenden Circigonia Icosahedra und den Circorhegma Dodecahedra mit seinem Dodecaeder-förmigen Skelett anführen. (17)

Die Goldene Proportion in der in DNS

Auch die Moleküle, in denen alle physischen Eigenschaften der Lebewesen gespeichert sind, wurden in einer auf der Goldenen Proportion basierenden Form erschaffen. Das DNS Molekül, das Programm des Lebens, basiert auf der Goldenen Proportion. Die DNS besteht aus zwei umeinander gewickelten stabförmigen Helixen. Die Länge der Krümmung der beiden Helixen ist 34 Angström und deren Breite 21 Angström. (1 Angström ist ein Hundert-Millionstel eines Zentimeters) 21 und 34 sind zwei aufeinander folgende Fibonacci Zahlen.

Die Goldene Proportion bei Schneeflocken

Die Goldene Proportion erscheint auch in Kristallstrukturen. Die meisten sind zu winzig, um mit dem bloßen Auge erkannt zu werden. Doch man kann die Goldene Proportion in Schneeflocken erkennen. Die verschiedenen langen und kurzen Variationen und Vorsprünge einer Schneeflocke folgen der Goldenen Proportion. (18)

DIE GOLDENE PROPORTION IM ALL

Es gibt viele spiralförmige Galaxien im Universum, die die Goldene Proportion in Ihren Strukturen aufweisen.

Die Goldene Proportion in der Physik

Die Fibonacci Reihe und die Goldene Proportion tauchen auch in der Physik auf.

Wenn Licht auf zwei übereinanderliegende Schichten Glas fällt, durchdringt ein Teil des Lichts das Glas, ein Teil wird absorbiert und ein Teil wird reflektiert. Was hier passiert, ist eine mehrfache Reflexion. Die Zahl der Wege, die ein Lichtstrahl innerhalb des Glases nimmt, hängt von der Zahl seiner Reflexionen ab. Die Zahl der Lichtstrahlen, die wieder auftauchen, passt in die Fibonacci Reihe. (19)

Die Tatsache, dass die Form so vieler voneinander unabhängiger belebter und unbelebter Strukturen in der Natur einer bestimmten mathematischen Formel entspricht, ist einer der klarsten Beweise, dass diese Strukturen besonders erschaffen wurden. Die Goldene Proportion ist eine bekannte, von Künstlern angewandte Regel. Kunstwerke, die auf dieser Regel basieren, repräsentieren ästhetische Perfektion. Pflanzen, Galaxien, Mikro-Organismen, Kristalle und Lebewesen, die entsprechend dieser Regel designed sind und von Künstlern imitiert werden, sind Beweise für Allah’s überlegene Kunstfertigkeit. Allah offenbart im Qur’an, dass Er alle Dinge nach einem bestimmten Maß geschaffen hat:

... Allah hat allem sein Maß bestimmt. (Surat 65:3 - at-Talaq)

… Und jedes Ding hat bei Ihm sein Maß und Ziel.. (Surat 13:8 - ar-Ra‘d)

 

---

1- Mehmet Suat Bergil, Doðada/Bilimde/Sanatta, Altýn Oran (The Golden Ratio in Nature/Science/Art), Arkeoloji ve Sanat Yayinlari, 2nd Edition, 1993, p. 155.
2- Guy Murchie, The Seven Mysteries of Life, First Mariner Boks, New York, pp. 58-59.
3- J. Cumming, Nucleus: Architecture and Building Construction, Longman, 1985.
4- Mehmet Suat Bergil, Doðada/Bilimde/Sanatta, Altýn Oran (The Golden Ratio in Nature/Science/Art), Arkeoloji ve Sanat Yayinlari, 2nd Edition, 1993, p. 87.
5- A. L. Goldberger, et al., "Bronchial Asymmetry and Fibonacci Scaling." Experientia, 41 : 1537, 1985.
6- E. R. Weibel, Morphometry of the Human Lung, Academic Press, 1963.
7- William Charlton, Aesthetics: An Introduction, Hutchinson University Library, London, 1970.
8- Mehmet Suat Bergil, Doðada/Bilimde/Sanatta, Altýn Oran (The Golden Ratio in Nature/Science/Art), Arkeoloji ve Sanat Yayinlari, 2nd Edition, 1993, p. 77.
9- "The 'Golden' spirals and 'pentagonal' symmetry in the alive Nature," online at: http://www.goldenmuseum.com/index_engl.html
10- D'Arcy Wentworth Thompson, On Growth and Form, C.U.P., Cambridge, 1961.
11- C. Morrison, Along The Track, Withcombe and Tombs, Melbourne.
12- "The 'Golden' spirals and 'pentagonal' symmetry in the alive Nature," online at: http://www.goldenmuseum.com/index_engl.html
13- J. H. Mogle, et al., "The Stucture and Function of Viruses," Edward Arnold, London, 1978.
14- A. Klug, "Molecules on Grand Scale," New Scientist, 1561:46, 1987.
15- Mehmet Suat Bergil, Doðada/Bilimde/Sanatta, Altýn Oran (The Golden Ratio in Nature/Science/Art), Arkeoloji ve Sanat Yayinlari, 2nd Edition, 1993, p. 82.
16- Mehmet Suat Bergil, Doðada/Bilimde/Sanatta, Altýn Oran (The Golden Ratio in Nature/Science/Art), Arkeoloji ve Sanat Yayinlari, 2nd Edition, 1993, p. 85.
17- For bodies of radiolarians, see H. Weyl, Synnetry, Princeton, 1952.
18- Emre Becer, "Biçimsel Uyumun Matematiksel Kuralý Olarak, Altýn Oran" (The Golden Ratio as a Mathematical Rule of Formal Harmony), Bilim ve Teknik Dergisi (Journal of Science and Technology), January 1991, p.16.
19- V.E. Hoggatt, Jr. and Bicknell-Johnson, Fibonacci Quartley, 17:118, 1979.